Leet Code 1: Two Sum

Find the problem here. It's best to first attempt the problem before referring to any online solution or walkthrough, as the best teacher is hands-on experience.

Problem Breakdown

The problem is presented with these three pre-requisites:

1. Given an array of integers nums and an integer target, return indices of the two numbers such that they add up to target.
2. You may assume that each input would have exactly one solution, and you may not use the same element twice.
3. You can return the answer in any order.

Natural Approach

First, let's break down what this problem is asking, step by step. In instruction number 1, the statement reads that this problem takes two inputs:

1. [int] nums
2. int target

And must return the index of two numbers in nums that add up to target. Here's a quick example:

In this example, our array of integers n has 5 elements, two of which are guaranteed to sum to our target (t) of 10. Scanning this with our eyes, we can see the solution is to combine 4 and 6 in indices 0 and 2, which when combined sum to 10.

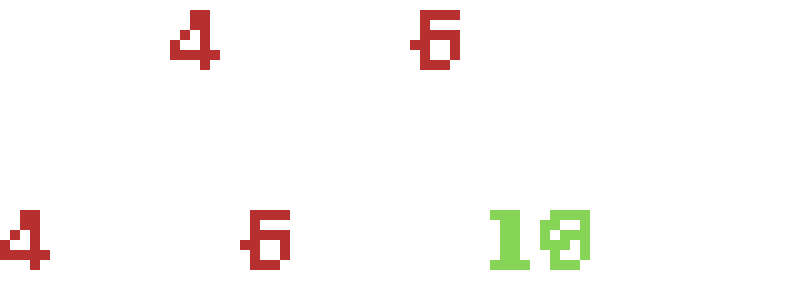
Therefore, we should return the indices pair [0, 2].

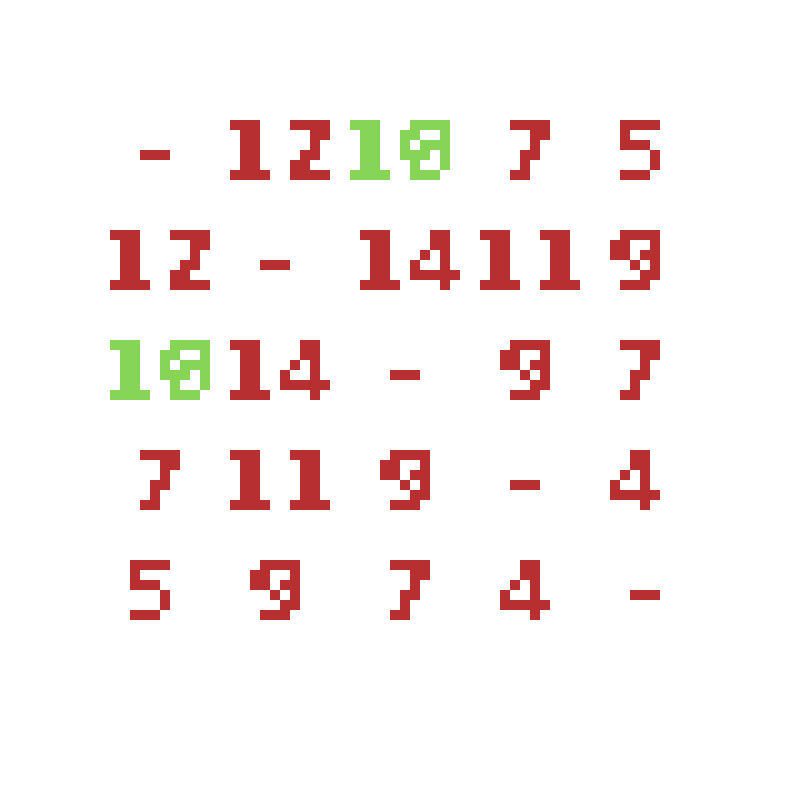
How did you solve this problem just now? You probably just 'eyeballed' it, and given your many years of experience solving math problems you intuitively know what numbers sum to 10. But if we were not given such a trivial example, and instead had an array of nums with 1000+ elements containing numbers greater than 100, our human intuition would quickly breakdown and we'd need to start solving it systematically. The simpliest, and most obvious approach, would be to create a table of every combination of numbers.

Note that I put a '-' for every combination of numbers where we'd be summing the same number twice, as this is not a valid solution to two-sum.

With this table, we can see clearly the answer occurs when 4 + 6 are summed. In fact, looking at it this way, we can see the answer appears twice; while this may seem obvious, file this detail away as we will use it later.

The next question I want you to ask yourself is this: how long will this approach take? We are checking every combination, and in doing so we have to check 5 combinations for 5 numbers.

Where n is the number of elements (5 in this case), we check n times, n times. Otherwise known as n^2.

However, we don't always check n^2 (25) times. As you can see in this example, we only check 3 times.

To understand why this n^2 figure is important, you have to first understand one very important metric for determining the speed of algorithms: run time complexity. Run time complexity is also referred to as big O notation, and you'll often see it written like this:

complexity : O(n^2)

Meaning in the worst case, this algorithmic approach will take n^2 iterations to complete. In this case, if the target were to be 4, it would take significantly longer to arrive at a solution.

Brute Force Solution

What we have just done is referred to as a "brute force" approach, where we check every possible combination of solutions in order to find the correct one. This approach will yield answer, but not quickly. Here's what this looks like in Python:

class Solution:
    def twoSum(self, nums: List[int], target: int) -> List[int]:
        for i, x in enumerate(nums):
            for j, y in enumerate(nums):
                if i != j:
                    sum = x + y
                    if sum == target:
                        return [i, j]

Note the usage of two for loops. This is a key indicator of the runtime complexity, in this case n^2.

This approach loops over the list of integers, nums, twice, and given that the indices don't overlap (to avoid summing the same number twice), we sum the two numbers together and see if they are our target. If they are, we return the two indices that combined to create the solution.

Again, this solution is correct, and will arrive at a correct answer eventually. It's a great starting point, and if you arrived at this answer then you have done an excellent job getting here. However, we can do better than this.

O(n) Solution

What if I told you we could completely eliminate an entire for loop? That would bring the runtime complexity of this problem down to O(n), which is n times faster than the last approach. And even better, it's the exact same number of lines of code.

First, I want to describe the reasoning behind this approach. We are checking every element twice to see if it sums to the target. However, we are ignoring a powerful data structure we could be using that can drastically speed this process up: a hash table. I'd strongly suggest you research what a hash table is if you don't know what it does, but I'll do my best to give you a quick explanation of the power of this data structure.

First, understand that looking up an item in a list will take at most n times. In the below example, if I wanted to retrieve 4 from this list, it would take me 4 iterations to find it.

Note that the 0, 1, 2, 3, 4 shown in the image is the index of that element.

It's for this reason that lists are very bad for retrieval. However, they are good for other things, which we will cover later.

With a hashtable, I can re-organize this data into a format much more effective for looking up data.

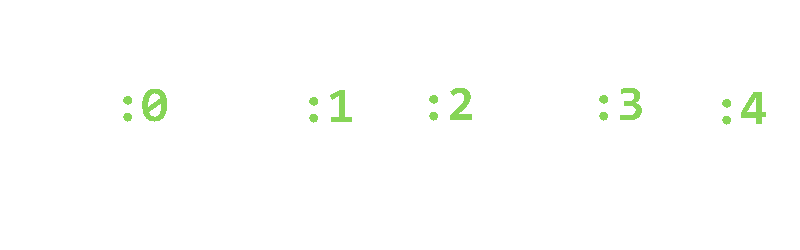
In this, I've reformatted my data into a hash table. A hash table is comprised of any number of key : value pairs. In this case, my key is the number, and my value is the index it appeared at in the list.

To enumerate it in code view:

{
    1 : 0,
    15: 1,
    5: 2,
    31: 3,
    4: 4
}

The above is what my hashtable would look like. If I wanted to check if 4 existed, it would be an O(1) look-up operation. This is insanely powerful, as this mean that checking if 4 exists can be done in constant time.

To do this in Python looks like this:

my_hash_table = {
    1 : 0,
    15: 1,
    5: 2,
    31: 3,
    4: 4
}

if 4 in my_hash_table:
    print("That was fast!")

This brings me back to our O(n) solution, which utilizes the power of a hash table to bring our time complexity down significantly.

prevNums = {}
for i, x in enumerate(nums):
    targetVal = target - x
        if targetVal in prevNums:
            return [i, prevNums[targetVal]]
        if x not in prevNums:
            prevNums[x] = i

Note there is only one for loop used, which is an indicator of the runtime, O(n) in this case.

Here's the rationale behind this solution.

Every number I encounter, I will insert into my hash table (called prevNums) in this fashion:

{
    key=value_at_this_index, value=index
}

This way, I can quickly look up any number I want in this hash table to see if I've seen it.

Now, what number do I want to look up? Given any number in this list, and the target value I want to arrive at, I can subract this number from the target to get the other value I need to find to arrive at a solution. This is called "targetVal" in the code. All I have to do now is compute this targetVal, and check the prevNums hash table to see if I've already encountered that number.

If I did see that number, I return my current index in the loop and the value of that key in the hash table (remember, this is configured to be the index of the value). And that's a wrap.

But how does this guarantee a solution? Well, remember a while back, I pointed out that the solution will always be arrived at twice. That's because both numbers could be flipped, and the answer could still be arrived at.

Using this knowledge, we know that we are guaranteed to find an answer, since even when we miss the solution on the first number of the correct pair (on number 4, checking to see if 6 exists in the prevNums hash table), we will always get it on the second number (on number 6, checking to see if 4 exists in the hash table).

Runtime

Check out the difference in runtime between these two algorithms. The brute force approach gets a runtime of 5451 ms on Leetcode, while the hash table approach gets a runtime of 58 ms. That's an insane difference, and really highlights the speed increase you get when optimizing an algorithm from O(n^2) down to O(n).

Closing notes

I hope this was a helpful illustration of how to solve two-sum. I want to reiterate that this approach was iterative: we started with a slower solution, and improved it into a much faster solution. Improving on your own work is a great skill to possess, as it requires you to be critical of yourself and accept that your first answer is not necessarily the best answer. If you have any questions, please reach out to me via LinkedIn or post it in the Discord. IF you have revisions you'd like to suggest, please feel free to either create an issue in the github repository (all of this material is open source and free) or create a pull request.

Thanks,

-Colt